在Coursera上学习吴恩达的DeepLearning.ai时遇到了一个疑惑——为什么一定要深度学习? 为什么要添加多个隐藏层?吴恩达给出了两种解释:1. 类比人脑, 越靠近输入的层学习越简单的特征,越靠近输出的层将前面各层的特征组合起来学习更加复杂的特征。2. 电路理论。
电路理论
There are functions you can compute with a “small” L-layer deep nerual network that shallower networks require exponentiall more hidden units to compute.
例如异或操作:
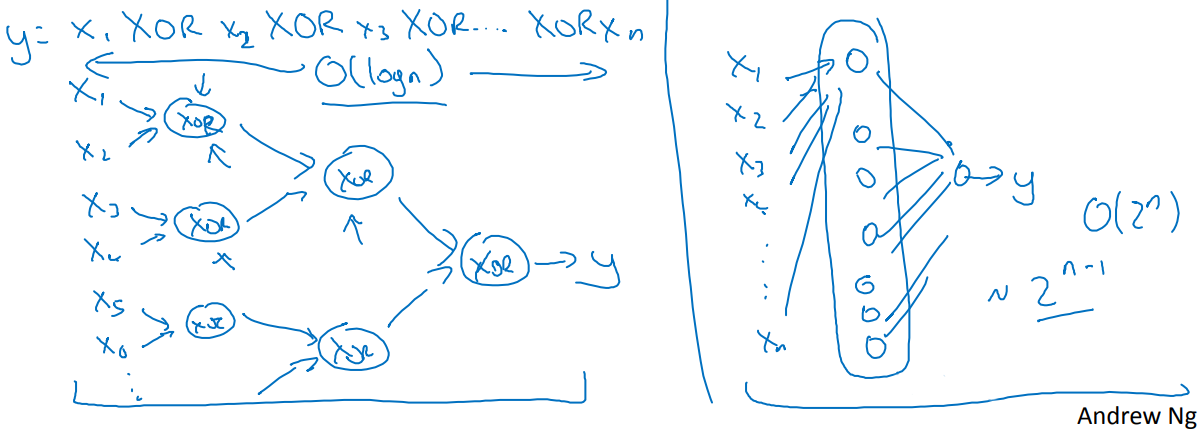
其中第一种解释很直观,第二种解释虽然直觉上是认可的,但应该有更通俗明白的解释。
假设输入三位数据$x_1x_2x_3$(e.g. 001), 采用深层网络可以拟合为$x_1⊕x_2⊕x_3$,而浅层网络拟合成什么样呢?这个时候就需要借助数电中根据真值表写逻辑表达式的技巧。
真值表如下
| $x_1$ | $x_2$ | $x_3$ | True Value |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
所以浅层网络推导为:
$x_1⋅x_2⋅x_3+x_1′⋅x_2′⋅x_3+x_1′⋅x_2⋅x_3′+x_1⋅x_2′⋅x_3′$
显然,深层网络需要的电子器件数为$O(logn)$, 而浅层网络需要$2^{n-1}$指数数量的器件,深层网络的拟合能力要远远强于浅层网络。