常用数据结构和算法模板(python)
经典
1.埃拉托斯特尼筛法
1 | def countPrimes(n): |
参考习题 https://leetcode-cn.com/problems/count-primes/, 答案如下,和模板略有区别:
1 | class Solution: |
2. 快速幂
1 | def myPow(x: float, n: int) -> float: |
练习题:https://leetcode-cn.com/problems/powx-n/
1 | class Solution: |
3. 大数模拟
大数加法
练习题:leetcode 415 https://leetcode-cn.com/problems/add-strings/
1 | def addStrings(self, num1: str, num2: str) -> str: |
大数乘法
练习题:leetcode 43 https://leetcode.com/problems/multiply-strings/
1 | def multiply(num1, num2): |
计算进位: 计算 carry = tmp // 10,代表当前位相加是否产生进位;
添加当前位: 计算 tmp = n1 + n2 + carry,并将当前位 tmp % 10 添加至 res 头部;
索引溢出处理: 当指针 i或j 走过数字首部后,给 n1,n2 赋值为 00,相当于给 num1,num2 中长度较短的数字前面填 00,以便后续计算。
当遍历完 num1,num2 后跳出循环,并根据 carry 值决定是否在头部添加进位 11,最终返回 res 即可。
复杂度分析:
时间复杂度 O(max(M,N))O(max(M,N)):其中 MM,NN 为 22 数字长度,按位遍历一遍数字(以较长的数字为准);
空间复杂度 O(1)O(1):指针与变量使用常数大小空间。
4. GCD
1 | def gcd(a, b): |
参考习题:https://leetcode-cn.com/problems/simplified-fractions/,最简分数,gcd的应用
1 | class Solution: |
5. LCM (最小公倍数)
1 | def lcm(a, b): |
7. 二分搜索
万能模板
1 | # 当分支逻辑不能排除右边界,选左中位数,如果选右中位数则会出现死循环 |
8. 并查集
1 | parent = list(range(N)) |
类形式:
1 | class DSU: |
图论
9. 最小生成树(贪心思想)
解析 花花酱:https://www.youtube.com/watch?v=wmW8G8SrXDs
图论500 题 https://blog.csdn.net/luomingjun12315/article/details/47438607
Kruskal算法

主体部分如下,需要用到并查集(下面完整测试案例中会给出)
1 | def kruskal(): |
leetcode中缺少相关的习题,固用花花酱视频中的例子测试了一下:
1 | n = 4 |
Prim算法

1 | def prime(): |
测试代码:
1 | from collections import defaultdict |
最短路算法合集
统一习题:LC743 https://leetcode-cn.com/problems/network-delay-time/
最短路算法的分类:
- 单源最短路
- 所有边权都是正数
- 朴素的Dijkstra算法 O(n^2) 适合稠密图
- 堆优化版的Dijkstra算法 O(mlog n)(m是图中节点的个数)适合稀疏图
- 存在负权边
- Bellman-Ford O(nm)
- spfa 一般O(m), 最坏O(nm)
- 所有边权都是正数
- 多源汇最短路 Floyd算法 O(n^3)
11. 迪杰斯特拉算法
单源最短路
- 所有边权都是正数
- 朴素的Dijkstra算法 O(n^2) 适合稠密图
- 堆优化版的Dijkstra算法 O(mlog n)(m是图中节点的个数)适合稀疏图
1 | def dijkstra(graph, source, N): |
习题解答:
1 | class Solution: |
Bellman-Ford 算法
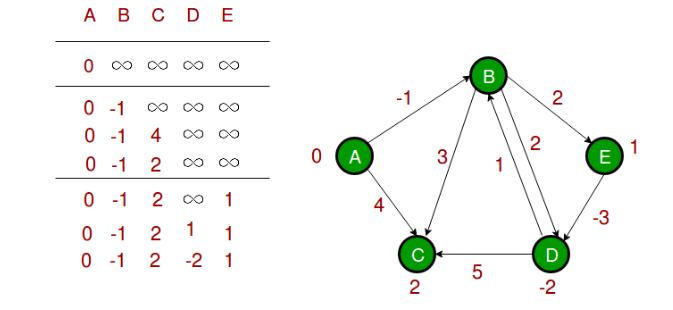
1 | # Python3 program for Bellman-Ford's single source |
1 | class Solution: |
12. spfa
判断有无负环:如果某个点进入队列的次数超过N次则存在负环(SPFA无法处理带负环的图,但是可以判断是否出现负权环)
1 | class Solution: |
13. Floyd-Warshall
1 | def floyd_warshall(graph, N): |
习题答案:
1 | class Solution: |
二分图
14. 染色法
1 | import collections |
15. 匈牙利算法 (用于寻找最大匹配)
讲解:https://www.renfei.org/blog/bipartite-matching.html
https://blog.csdn.net/dark_scope/article/details/8880547
1 | class DFS_hungary(): |
动态规划
16. 背包问题
reference:https://zhuanlan.zhihu.com/p/93857890
0-1背包
- 不装入第i件物品,即
dp[i−1][j]; - 装入第i件物品(前提是能装下),即
dp[i−1][j−w[i]] + v[i]。
即状态转移方程为
1 | dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i]]+v[i]) // j >= w[i] |
由上述状态转移方程可知,dp[i][j]的值只与dp[i-1][0,...,j-1]有关,所以我们可以采用动态规划常用的方法(滚动数组)对空间进行优化(即去掉dp的第一维)。需要注意的是,为了防止上一层循环的dp[0,...,j-1]被覆盖,循环的时候 j 只能逆向枚举(空间优化前没有这个限制),伪代码为:
1 | // 01背包问题伪代码(空间优化版) |
动态规划的核心思想避免重复计算在01背包问题中体现得淋漓尽致。第i件物品装入或者不装入而获得的最大价值完全可以由前面i-1件物品的最大价值决定,暴力枚举忽略了这个事实。
完全背包
分析一
- 不装入第i种物品,即
dp[i−1][j],同01背包; - 装入第i种物品,此时和01背包不太一样,因为每种物品有无限个(但注意书包限重是有限的),所以此时不应该转移到
dp[i−1][j−w[i]]而应该转移到dp[i][j−w[i]],即装入第i种商品后还可以再继续装入第种商品。
所以状态转移方程为
1 | dp[i][j] = max(dp[i−1][j], dp[i][j−w[i]]+v[i]) // j >= w[i] |
这个状态转移方程与01背包问题唯一不同就是max第二项不是dp[i-1]而是dp[i]。
和01背包问题类似,也可进行空间优化,优化后不同点在于这里的 j 只能正向枚举而01背包只能逆向枚举,因为这里的max第二项是dp[i]而01背包是dp[i-1],即这里就是需要覆盖而01背包需要避免覆盖。所以伪代码如下:
1 | // 完全背包问题思路一伪代码(空间优化版) |
由上述伪代码看出,01背包和完全背包问题此解法的空间优化版解法唯一不同就是前者的 j 只能逆向枚举而后者的 j 只能正向枚举,这是由二者的状态转移方程决定的。此解法时间复杂度为O(NW), 空间复杂度为O(W)。
分析二
除了分析一的思路外,完全背包还有一种常见的思路,但是复杂度高一些。我们从装入第 i 种物品多少件出发,01背包只有两种情况即取0件和取1件,而这里是取0件、1件、2件…直到超过限重(k > j/w[i]),所以状态转移方程为:
1 | # k为装入第i种物品的件数, k <= j/w[i] |
同理也可以进行空间优化,需要注意的是,这里max里面是dp[i-1],和01背包一样,所以 j 必须逆向枚举,优化后伪代码为
1 | // 完全背包问题思路二伪代码(空间优化版) |
相比于分析一,此种方法不是在O(1)时间求得dp[i][j],所以总的时间复杂度就比分析一大些了,为 级别。
分析三、转换成01背包
01背包问题是最基本的背包问题,我们可以考虑把完全背包问题转化为01背包问题来解:将一种物品转换成若干件只能装入0件或者1件的01背包中的物品。
最简单的想法是,考虑到第 i 种物品最多装入 W/w[i] 件,于是可以把第 i 种物品转化为 W/w[i] 件费用及价值均不变的物品,然后求解这个01背包问题。
更高效的转化方法是采用二进制的思想:把第 i 种物品拆成重量为 、价值为
的若干件物品,其中 k 取遍满足
的非负整数。这是因为不管最优策略选几件第 i 种物品,总可以表示成若干个刚才这些物品的和(例:13 = 1 + 4 + 8)。这样就将转换后的物品数目降成了对数级别。
多重背包
分析一
此时的分析和完全背包的分析二差不多,也是从装入第 i 种物品多少件出发:装入第i种物品0件、1件、…n[i]件(还要满足不超过限重)。所以状态方程为:
1 | # k为装入第i种物品的件数, k <= min(n[i], j/w[i]) |
同理也可以进行空间优化,而且 j 也必须逆向枚举,优化后伪代码为
1 | // 完全背包问题思路二伪代码(空间优化版) |
总的时间复杂度约为 级别。
其他情形
参考https://blog.csdn.net/weixin_41162823/article/details/87878853
1 恰好装满
背包问题有时候还有一个限制就是必须恰好装满背包,此时基本思路没有区别,只是在初始化的时候有所不同。
如果没有恰好装满背包的限制,我们将dp全部初始化成0就可以了。因为任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始时状态的值也就全部为0了。如果有恰好装满的限制,那只应该将dp[0,…,N][0]初始为0,其它dp值均初始化为-inf,因为此时只有容量为0的背包可以在什么也不装情况下被“恰好装满”,其它容量的背包初始均没有合法的解,应该被初始化为-inf。
2 求方案总数
除了在给定每个物品的价值后求可得到的最大价值外,还有一类问题是问装满背包或将背包装至某一指定容量的方案总数。对于这类问题,需要将状态转移方程中的 max 改成 sum ,大体思路是不变的。例如若每件物品均是完全背包中的物品,转移方程即为
1 | dp[i][j] = sum(dp[i−1][j], dp[i][j−w[i]]) // j >= w[i] |
3 二维背包
前面讨论的背包容量都是一个量:重量。二维背包问题是指每个背包有两个限制条件(比如重量和体积限制),选择物品必须要满足这两个条件。此类问题的解法和一维背包问题不同就是dp数组要多开一维,其他和一维背包完全一样,例如5.4节。
4 求最优方案
一般而言,背包问题是要求一个最优值,如果要求输出这个最优值的方案,可以参照一般动态规划问题输出方案的方法:记录下每个状态的最优值是由哪一个策略推出来的,这样便可根据这条策略找到上一个状态,从上一个状态接着向前推即可。
以01背包为例,我们可以再用一个数组G[i][j]来记录方案,设 G[i][j] = 0表示计算 dp[i][j] 的值时是采用了max中的前一项(也即dp[i−1][j]),G[i][j] = 1 表示采用了方程的后一项。即分别表示了两种策略: 未装入第 i 个物品及装了第 i 个物品。其实我们也可以直接从求好的dp[i][j]反推方案:若 dp[i][j] = dp[i−1][j] 说明未选第i个物品,反之说明选了。
Leetcode相关练习题
0 - 1 背包问题:416. 分割等和子集
题目给定一个只包含正整数的非空数组。问是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
由于所有元素的和sum已知,所以两个子集的和都应该是sum/2(所以前提是sum不能是奇数),即题目转换成从这个数组里面选取一些元素使这些元素和为sum/2。如果我们将所有元素的值看做是物品的重量,每件物品价值都为1,所以这就是一个恰好装满的01背包问题。
我们定义空间优化后的状态数组dp,由于是恰好装满,所以应该将dp[0]初始化为0而将其他全部初始化为INT_MIN,然后按照类似1.2节的伪代码更新dp:
1 | int capacity = sum / 2; |
更新完毕后,如果dp[sum/2]大于0说明满足题意。
由于此题最后求的是能不能进行划分,所以dp的每个元素定义成bool型就可以了,然后将dp[0]初始为true其他初始化为false,而转移方程就应该是用或操作而不是max操作。完整代码如下:
1 | class Solution: |
完全背包问题:322. 零钱兑换
题目给定一个价值amount和一些面值,假设每个面值的硬币数都是无限的,问我们最少能用几个硬币组成给定的价值。
如果我们将面值看作是物品,面值金额看成是物品的重量,每件物品的价值均为1,这样此题就是是一个恰好装满的完全背包问题了。不过这里不是求最多装入多少物品而是求最少,我们只需要将2.2节的转态转移方程中的max改成min即可,又由于是恰好装满,所以除了dp[0],其他都应初始化为INT_MAX。完整代码如下:
1 | class Solution: |
17. 最长上升子序列
1 | class Solution: |
贪心加二分优化:
1 | class Solution: |
18. 最长公共子序列
1 | class Solution: |
字符串
26. KMP 字符串匹配
练习题 https://leetcode.com/problems/implement-strstr/
1 | # Python program for KMP Algorithm |
27. 字典树
练习题:https://leetcode.com/problems/implement-trie-prefix-tree/
1 | class TrieNode: |
区间查询
29. 线段树
1 | class Node: |
30. 树状数组
1 | class FenwickTree: |